Computational Locality in Nonlinear Morphophonology
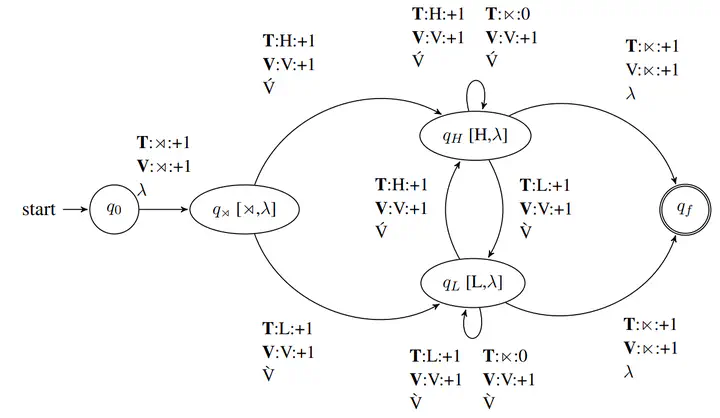
Abstract
This paper presents a computational analysis of locality in nonlinear phonology and morphology. Most segmental phonology and concatenative morphology are computationally local and characterized by the class of Input Strictly Local functions. We generalize these functions to consider multiple inputs, i.e. Multi-Input Strictly Local. We implement this approach using multi-tape automata, and find that they elegantly characterize the bulk of nonlinear suprasegmental phonology and morphology. We demonstrate these results for both tonal phonology and template-filling patterns in root-and-pattern morphology. We show that locality is affected by some theoretical choices (directionality, tier-conflation), but not others (phonological content of templates). For prosodic morphology, nuanced representational choices can affect locality. The flexibility and precision given by the mathematical theory of formal languages provides precise discussion of the nuances of phonological and morphological complexity and substance in a theory-independent but rigorous way.