Regular and Polyregular Theories of Reduplication

Abstract

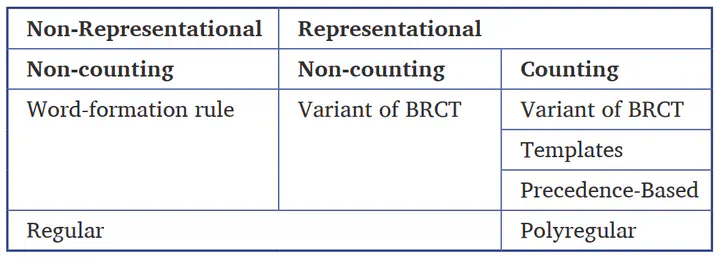
We explore the generative capacity of morphological theories of reduplication. We computationally classify theories of reduplication using a hierarchy of string-to-string function classes. Reduplication as a process requires only the regular class of functions. We show that various morphological theories necessarily treat it as a more expressive polyregular function, while others maintain regularity. We discuss the significance of this formal result for reduplicative functions and recognition.

Jon Rawski

Assistant Professor of Linguistics